MATLAB快速入门(四)
一.简介
本篇参考官方入门文档编写
前提准备:
- MATLAB
二. 快速入门(四)
1. 输入命令
format 函数
format 函数控制所显示的值的数值格式。此函数仅影响数字显示方式,而不会影响 MATLAB® 软件如何计算或保存数字。下面提供了不同格式及由向量 x 生成的最终输出,该向量的各个分量具有不同的量值。
注意
为了确保适当的间隔,请使用等宽字体,例如 Courier。
1 | x = [4/3 1.2345e-6] |
如果矩阵的最大元素大于 103 或小于 10-3,MATLAB 会对短格式和长格式应用常用缩放因子。
除了上面显示的 format 函数,
1 | format compact |
会不显示在输出中出现的多个空行。这样,您可以在屏幕或窗口中查看更多信息。如果要进一步控制输出格式,请使用 sprintf 和 fprintf 函数。
隐藏输出
如果您在仅键入语句后按 Return 或 Enter,MATLAB 会在屏幕上自动显示结果。但是,如果使用分号结束行,MATLAB 会执行计算,但不会显示任何输出。当生成大型矩阵时,此功能尤其有用。例如,
1 | A = magic(100); |
输入长语句
如果语句无法容纳在一行中,请使用省略号(三个句点)...,后跟 Return 或 Enter 以指示该语句在下一行继续。例如,
1 | s = 1 -1/2 + 1/3 -1/4 + 1/5 - 1/6 + 1/7 ... |
=、+ 和 - 符号周围的空白是可选的,但可提高可读性。
命令行编辑
使用键盘上的各个箭头键和控制键可以重新调用、编辑和重用先前键入的语句。例如,假定您错误地输入了
1 | rho = (1 + sqt(5))/2 |
sqrt 的拼写不正确。MATLAB 会给出以下错误信息
1 | Undefined function 'sqt' for input arguments of type 'double'. |
您只需按 ↑ 键,而不必重新键入整行。系统将重新显示键入的语句。使用 ← 键移动光标并插入缺少的 r。反复使用 ↑ 键可重新调用前面的行。键入几个字符并按 ↑ 键可查找前文中以这些字符开头行。还可以从命令历史记录中复制以前执行的语句。
2. 索引
下标
A 的行 i 和列 j 中的元素通过 A(i,j) 表示。例如,A(4,2) 表示第四行和第二列中的数字。在幻方矩阵中,A(4,2) 为 15。因此,要计算 A 第四列中的元素的总和,请键入
1 | A(1,4) + A(2,4) + A(3,4) + A(4,4) |
此下标生成
1 | ans = |
但这不是计算某列总和的最佳方法。
此外,还可以使用单一下标 A(k) 引用矩阵的元素。单一下标是引用行和列向量的常见方法。但是,也可以对满二维矩阵应用单一下标。在这种情况下,数组被视为一个由原始矩阵的列构成的长列向量。因此,在幻方矩阵中,A(8) 是另一种引用存储在 A(4,2) 中的值 15 的方法。
如果尝试使用矩阵外部元素的值,则会生成错误:
1 | t = A(4,5) |
相反,如果将值存储在矩阵外部元素中,则会增大大小以便容纳新元素:
1 | X = A; |
冒号运算符
冒号 : 是最重要的 MATLAB® 运算符之一。它以多种不同形式出现。表达式
1 | 1:10 |
是包含从 1 到 10 之间的整数的行向量:
1 | 1 2 3 4 5 6 7 8 9 10 |
要获取非单位间距,请指定增量。例如,
1 | 100:-7:50 |
为
1 | 100 93 86 79 72 65 58 51 |
而
1 | 0:pi/4:pi |
为
1 | 0 0.7854 1.5708 2.3562 3.1416 |
包含冒号的下标表达式引用部分矩阵:
1 | A(1:k,j) |
表示 A 第 j 列中的前 k 个元素。因此,
1 | sum(A(1:4,4)) |
计算第四列的总和。但是,执行此计算有一种更好的方法。冒号本身引用矩阵行或列中的所有元素,而关键字 end 引用最后一个行或列。因此,
1 | sum(A(:,end)) |
计算 A 最后一列中的元素的总和:
1 | ans = |
为什么 4×4 幻方矩阵的幻数和等于 34?如果将介于 1 到 16 之间的整数分为四个总和相等的组,该总和必须为
1 | sum(1:16)/4 |
当然,也即
1 | ans = |
串联
串联是连接小矩阵以便形成更大矩阵的过程。实际上,第一个矩阵是通过将其各个元素串联起来而构成的。成对的方括号 [] 即为串联运算符。例如,从 4×4 幻方矩阵 A 开始,组成
1 | B = [A A+32; A+48 A+16] |
结果会生成一个 8×8 矩阵,这是通过连接四个子矩阵获得的:
1 | B = |
此矩阵是一个接近于幻方矩阵的矩阵。此矩阵的元素是经过重新排列的整数 1:64。此矩阵的列总和符合 8×8 幻方矩阵的要求:
1 | sum(B) |
但是其行总和 sum(B')' 并不完全相同。要使其成为有效的 8×8 幻方矩阵,需要进行进一步操作。
删除行和列
只需使用一对方括号即可从矩阵中删除行和列。首先
1 | X = A; |
然后,要删除 X 的第二列,请使用
1 | X(:,2) = [] |
这会将 X 更改为
1 | X = |
如果您删除矩阵中的单个元素,结果将不再是矩阵。因此,以下类似表达式
1 | X(1,2) = [] |
将会导致错误。但是,使用单一下标可以删除一个元素或元素序列,并将其余元素重构为一个行向量。因此
1 | X(2:2:10) = [] |
生成
1 | X = |
标量扩展
可以采用多种不同方法将矩阵和标量合并在一起。例如,通过从每个元素中减去标量而将其从矩阵中减去。幻方矩阵的元素平均值为 8.5,因此
1 | B = A - 8.5 |
形成一个列总和为零的矩阵:
1 | B = |
通过标量扩展,MATLAB 会为范围中的所有索引分配一个指定标量。例如,
1 | B(1:2,2:3) = 0 |
将 B 的某个部分清零:
1 | B = |
逻辑下标
根据逻辑和关系运算创建的逻辑向量可用于引用子数组。假定 X 是一个普通矩阵,L 是一个由某个逻辑运算生成的同等大小的矩阵。那么,X(L) 指定 X 的元素,其中 L 的元素为非零。
通过将逻辑运算指定为下标表达式,可以在一个步骤中完成这种下标。假定您具有以下数据集:
1 | x = [2.1 1.7 1.6 1.5 NaN 1.9 1.8 1.5 5.1 1.8 1.4 2.2 1.6 1.8]; |
NaN 是用于缺少的观测值的标记,例如,无法响应问卷中的某个项。要使用逻辑索引删除缺少的数据,请使用 isfinite(x),对于所有有限数值,该函数为 true;对于 NaN 和 Inf,该函数为 false:
1 | x = x(isfinite(x)) |
现在,存在一个似乎与其他项很不一样的观测值,即 5.1。这是一个离群值。下面的语句可删除离群值,在本示例中,即比均值大三倍标准差的元素:
1 | x = x(abs(x-mean(x)) <= 3*std(x)) |
标量扩展对于另一示例,请使用逻辑索引和标量扩展将非质数设置为 0,以便高亮显示丢勒幻方矩阵中的质数的位置。(请参阅 magic 函数。)
1 | A(~isprime(A)) = 0 |
find 函数
find 函数可用于确定与指定逻辑条件相符的数组元素的索引。find 以最简单的形式返回索引的列向量。转置该向量以便获取索引的行向量。例如,再次从丢勒的幻方矩阵开始。(请参阅 magic 函数。)
1 | k = find(isprime(A))' |
使用一维索引选取幻方矩阵中的质数的位置:
1 | k = |
使用以下命令按 k 确定的顺序将这些质数显示为行向量
1 | A(k) |
将 k 用作赋值语句的左侧索引时,会保留矩阵结构:
1 | A(k) = NaN |
3. 数组类型
多维数组
MATLAB® 环境中的多维数组是具有多个下标的数组。创建多维数组的一种方法是调用具有多个参数的 zeros、ones、rand 或 randn。例如,
1 | R = randn(3,4,5); |
创建一个 3×4×5 数组,共包含 3*4*5 = 60 个正态分布的随机元素。
三维数组可表示在矩形网格中采样的三维物理数据,例如室内温度。或者也可以表示矩阵序列 A(k) 或与时间相关的矩阵示例 A(t)。在下面的示例中,第 k 个或第 tk 个矩阵的第 (i, j) 个元素由 A(i,j,k) 表示。
MATLAB 与丢勒的 4 阶幻方矩阵版本的区别在于交换了两个列。通过交换列,可以生成许多不同的幻方矩阵。语句
1 | p = perms(1:4); |
生成 4! = 24 置换1:4。第 k 个置换为行向量 p(k,:)。然后,
1 | A = magic(4); |
将含有 24 个幻方矩阵的序列存储在三维数组 M 中。M 大小为
1 | size(M) |
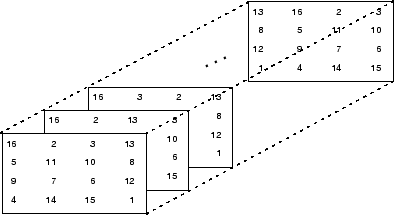
注意
此插图中显示的矩阵顺序可能不同于您的结果。perms 函数始终返回输入向量的所有置换,但置换顺序可能因不同 MATLAB 版本而异。
语句
1 | sum(M,d) |
通过改变第 d 个下标来计算总和。因此
1 | sum(M,1) |
是一个含有 24 个行向量副本的 1×4×24 数组
1 | 34 34 34 34 |
而
1 | sum(M,2) |
是一个含有 24 个列向量副本的 4×1×24 数组
1 | 34 |
最后,
1 | S = sum(M,3) |
在序列中添加 24 个矩阵。结果的大小为 4×4×1,因此它看似是 4×4 数组:
1 | S = |
元胞数组
MATLAB 中的元胞数组是以其他数组的副本为元素的多维数组。使用 cell 函数可以创建空矩阵的元胞数组。但是,更普遍的做法是,通过将其他内容的集合括入花括号 {} 中来创建元胞数组。花括号还可以与下标配合使用,以便访问各个元胞的内容。例如,
1 | C = {A sum(A) prod(prod(A))} |
生成一个 1×3 元胞数组。这三个元胞包含幻方矩阵、列总和的行向量及其所有元素的乘积。当显示 C 时,您会看到
1 | C = |
这是因为前两个元胞太大,无法在此有限空间中输出,但第三个元胞仅包含 16! 一个数字,因此有空间可以输出此数字。
请牢记以下两大要点。第一,要检索某个元胞的内容,请在花括号中使用下标。例如,C{1} 检索幻方矩阵,C{3} 为 16!。第二,元胞数组包含其他数组的副本,而不包含指向这些数组的指针。如果随后更改 A,C 不会发生变化。
使用三维数组可以存储相同大小的矩阵序列。元胞数组可用于存储不同大小的矩阵序列。例如,
1 | M = cell(8,1); |
生成具有不同顺序的幻方矩阵序列:
1 | M = |
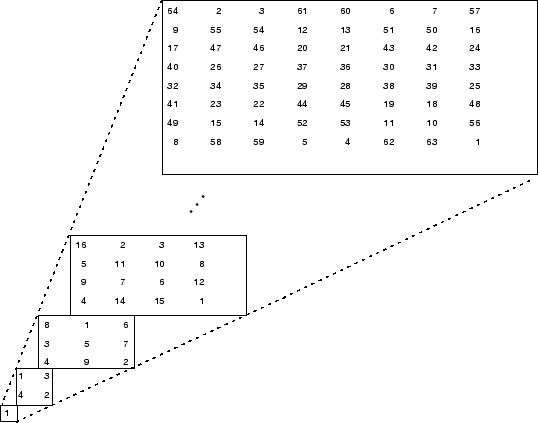
使用以下命令可以检索 4×4 幻方矩阵
1 | M{4} |
字符与文本
使用单引号在 MATLAB 中输入文本。例如,
1 | s = 'Hello' |
其结果与您目前已学过的数值矩阵或数组不属于同一类型,而是一个 1×5 字符数组。
字符在内部作为数字存储,而不会采用浮点格式存储。语句
1 | a = double(s) |
将字符数组转换为数值矩阵,该矩阵包含每个字符的 ASCII 代码的浮点表示。结果为
1 | a = |
语句
1 | s = char(a) |
是刚才转换的逆转换。
将数字转换为字符可以调查计算机上的各种可用字体。基本 ASCII 字符集中的可打印字符由整数 32:127 表示。(小于 32 的整数表示不可打印的控制字符。)这些整数使用以下语句按相应的 6×16 数组的形式排列
1 | F = reshape(32:127,16,6)'; |
扩展 ASCII 字符集中的可打印字符由 F+128 表示。将这些整数解释为字符时,结果取决于当前使用的字体。键入语句
1 | char(F) |
然后改变命令行窗口所用的字体。要更改字体,请在主页选项卡上的环境部分中,点击预设 > 字体。如果代码行中包含制表符,请使用等宽字体(例如,Monospaced)以便在不同行中对齐制表符位置。
使用方括号进行串联可将文本变量联接到一起。语句
1 | h = [s, ' world'] |
水平联接字符并生成
1 | h = |
语句
1 | v = [s; 'world'] |
垂直联接字符并生成
1 | v = |
请注意,必须在 h 中的 'w' 前插入一个空格,并且 v 中的两个单词的长度必须相同。生成的数组均为字符数组;h 为 1×11,v 为 2×5。
要操作包含不同长度的行的文本主体,您有两种选择,即使用填充的字符数组或使用字符向量元胞数组。创建字符数组时,数组各行的长度必须相同。(使用空格填充较短行的末尾。)char 函数可执行这种填充操作。例如,
1 | S = char('A','rolling','stone','gathers','momentum.') |
生成一个 5×9 字符数组:
1 | S = |
再者,您也可以将文本存储在元胞数组中。例如,
1 | C = {'A';'rolling';'stone';'gathers';'momentum.'} |
创建一个不需要任何填充的 5×1 元胞数组,因为该数组的各行可以具有不同的长度:
1 | C = |
使用以下语句可以将填充后的字符数组转换为字符向量元胞数组:
1 | C = cellstr(S) |
使用以下语句可以逆转此过程
1 | S = char(C) |
结构体
结构体是多维 MATLAB 数组,包含可按文本字段标志符访问的元素。例如,
1 | S.name = 'Ed Plum'; |
创建一个具有三个字段的标量结构体:
1 | S = |
与 MATLAB 环境中的所有其他内容一样,结构体也为数组,因此可以插入其他元素。在本示例中,数组的每个元素都是一个具有若干字段的结构体。可以一次添加一个字段,
1 | S(2).name = 'Toni Miller'; |
也可以使用一个语句添加整个元素:
1 | S(3) = struct('name','Jerry Garcia',... |
现在,结构体非常大以致仅输出摘要:
1 | S = |
将不同字段重新组合为其他 MATLAB 数组的方法有许多种。这些方法大多基于逗号分隔列表的表示法。键入
1 | S.score |
与键入
1 | S(1).score, S(2).score, S(3).score |
相同,这是一个逗号分隔列表。
如果将生成此类列表的表达式括在方括号中,MATLAB 会将该列表中的每一项都存储在数组中。在本示例中,MATLAB 创建一个数值行向量,该向量包含结构体数组 S 的每个元素的 score 字段:
1 | scores = [S.score] |
要根据某个文本字段(例如,name)创建字符数组,请对 S.name 生成的逗号分隔列表调用 char 函数:
1 | names = char(S.name) |
同样,通过将生成列表的表达式括入花括号中,可以根据 name 字段创建元胞数组:
1 | names = {S.name} |
要将结构体数组的每个元素的字段赋值给结构体外部的单独变量,请指定等号左侧的每个输出,并将其全部括在方括号中:
1 | [N1 N2 N3] = S.name |
动态字段名称
访问结构体中的数据的最常用方法是指定要引用的字段的名称。访问结构体数据的另一种方法是使用动态字段名称。这些名称将字段表示为变量表达式,MATLAB 会在运行时计算这些表达式。此处显示的点-括号语法将 expression 作为动态字段名称:
1 | structName.(expression) |
使用标准 MATLAB 索引语法创建此字段的索引。例如,要在字段名称中计算 expression,并在行 7 中的 1 至 25 列内获取该字段的值,请使用
1 | structName.(expression)(7,1:25) |
动态字段名称示例. 下面显示的 avgscore 函数可用于计算考试的平均分数,并使用动态字段名称检索 testscores 结构体中的信息:
1 | function avg = avgscore(testscores, student, first, last) |
您可以运行此函数,并对动态字段 student 使用不同值。首先,对包含 25 周内的分数的结构体进行初始化:
1 | testscores.Ann_Lane.week(1:25) = ... |
现在,运行 avgscore,并在运行时使用动态字段名称为 testscores 结构体提供学生姓名字段:
1 | avgscore(testscores, 'Ann_Lane', 7, 22) |





